Stable Seating

Problem Statement

We have $4n$ seats arranged in $4$ columns, $n$ rows and we want to seat $4n$ people in them in the best possible way (i.e. a group of $4$ friends who really like each other should be seated together).

Given $4n$ people, along with their ranking(/preference) for each other and whether they want middle or corner seat, seat them in $n$ rows in a “stable” manner.

Here, stable means that I got seated with the “best possible option that I had”. In particular, if I prefer some person X over my current partner, then X does not prefer me over their partner. In a graph, it would look something like this: 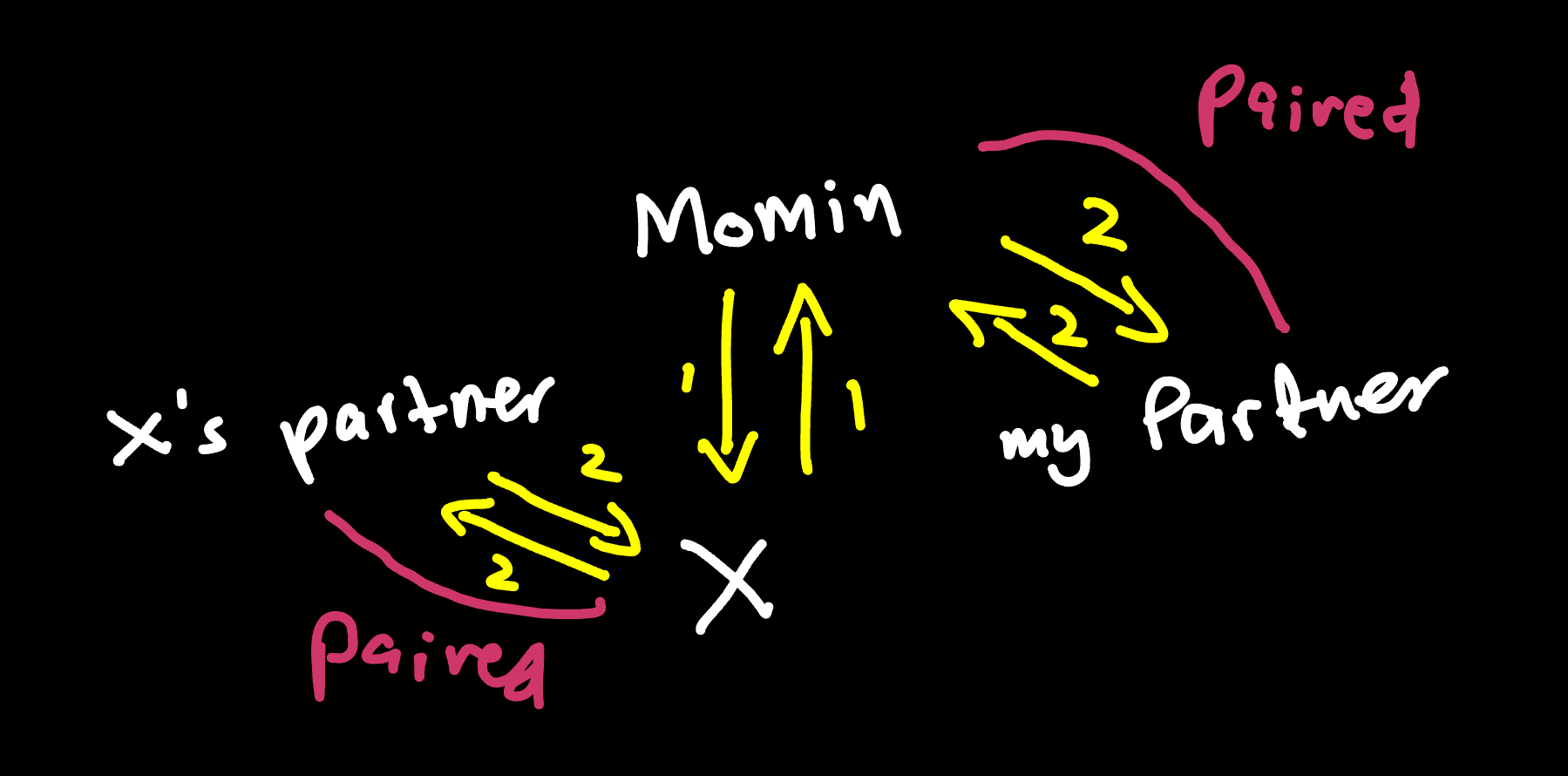This is not a stable seating because I would rather be with X and X would rather be with me so we have no reason to follow this seating.

This definition of stability is inspire by the popular “Stable Marriage Problem” and I also using the Gale-Shapely Algorithm designed for it - so let’s use take a look at the Stable Marriage Problem first.

Stable Marriage Problem & Gale-Shapely Algorithm

In this scenario, we have $n$ boys and $n$ girls and we want to find a stable marrage pairing (with the same definition of stability). Each girl has ranked the $n$ boys from most preference to least prefered and similarly, the boys also separately rank all $n$ girls.

The (apparently Nobel Prize winning) Gale-Shapely Algirthm gives a greedy $O(n^2)$ solution to this problem. And it goes as follows :

In Day1, each boy proposes to the girl that is their first preference. At the end of the day, each girl keeps the boy who they currently prefer the most and reject the other boys. Note that here it is not necessary that every girl gets proposed to.

In the next day, the rejected boys now propose to their second preference. At the end of the day, the girls follow the same procedure: They keep the current highest preference and reject the rest. And the process continuous …

It is easy to see that firstly this process terminates after at most day $n$ and also that it necessarily resuls in stable pairing of the boys and girls.

So, coming back to our problem, we can notice that this is exactly the scenario when we want to match the $2n$ corner seat people with the $2n$ middle seat people since we also have a bipartide graph.

So we apply the same algorithm and end up with $2n$ pairs. Now, we wish to pair the $2n$ middle seat people (which would give us seatings of $4$ since each middle seat person already has one corner seat neighbour). But you can notice here that the graph of middle seat people is a complete graph instead of a bipartide graph. It turns out, there is a very similar algorithm - Irving’s Algorithm - which deals with the analogous “Stable Roomate Problem”.

Stable Roomates Problem & Irving’s Algorithm

Consider the same problem as the previous, except now we have a complete graph - or in other words, same-sex pairing are now allowed. This problem is more popularly formulaed as “Stable Roomates Problems” :

Given $2n$ people, where each person ranks the other $2n-1$, and given $n$ rooms (each with capacity of $2$ people), find a stable roomates pairing.

The algorithm is fairly similar, and I am too lazy (and probably won’t do a good job explainig) so here’s a nice youtube video:

Firstly, this also runs in $O(n^2)$. More importantly, unlike Gale-Shapely, a stable matching may not exist since we can have a “love traingle”.

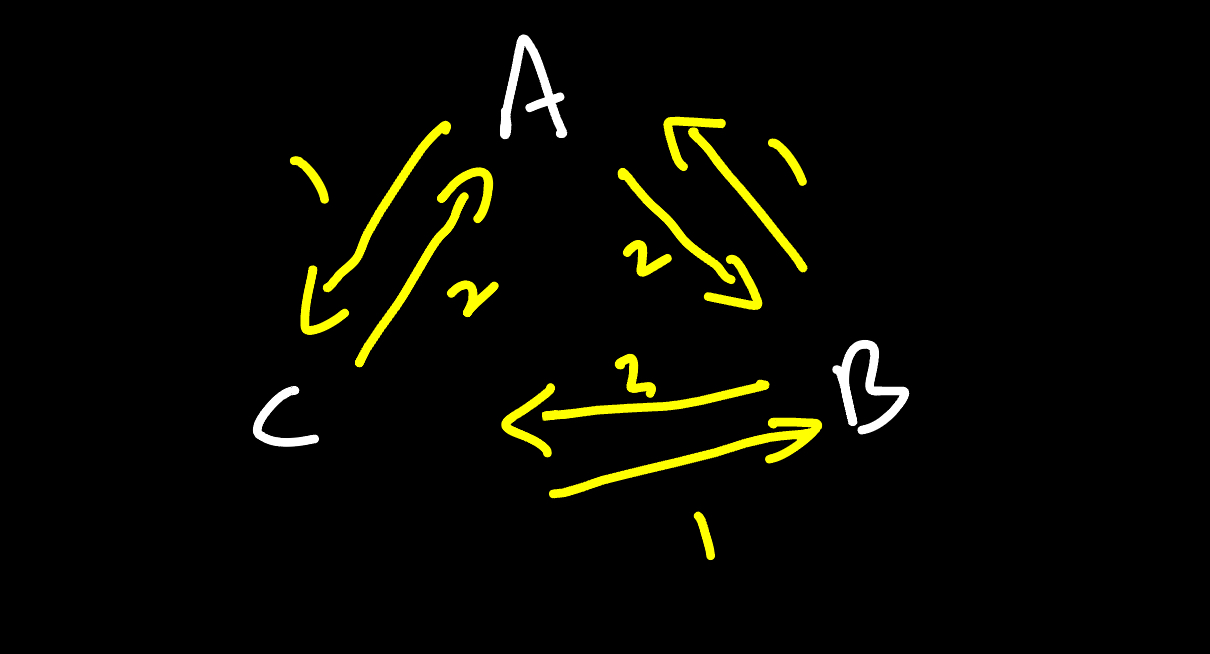
Here it is easy to see that no stable pairing exists. Essentially, if the preferences are really diverse (people do not replicate other’s feelings) then a stable pairing does not exist (which in real life is a bit unlikely - specially with larger $n$),

Back to our problem, we can finally use this to pair the middle seats and we are done!

Remarks About the Code

The code is avaiable on github here .

For anyone who wants to look at the code, please don’t. Practically, it is hard to code a less effecient program than this one. In my quest to add a GUI in C, I have thrown away all effeciency out of the window - even though, ironically, effeciency is what motivated to work on this.

I worked on this problem as an “End Semester Project” to an intro to CS class. The classroom was arranged in $4$ seats in each row and there was “free seating” i.e. you can sit where ever you want. So naturally, it begs the question - “What is the best possible seating”.

I hope this may be useful to someone in a similar scenario. As garbage as the code may be, it still works and will give the correct output :) .